Using Benfords Law to identify fake Bitcoin exchange transactions
Fake volumes
Bitcoin exchanges are booming -- on a weekly basis new exchanges appear out of nowhere, some already with considerable volume (for new exchanges). Clearly, every trader wants to trade on the most liquid exchange, as that exchange most likely has the best prices and fastest executions. Therefore there's a big incentive for new exchanges to attract liquidity somehow, either through a good fee structure or just by spending more money on marketing. For less honest exchanges there's another option: simply faking transaction data.
Recently, one of the bigger Chinese Bitcoin exchanges got accused of faking transaction data in order to appear more attractive than they really were.
Could you systematically find evidence for such fraud without having to have access to the internal accounting of such exchanges?
Benford's Law
There's a very unintuitive observation when it comes to a lot of types of data: count the occurrences of the leading digit of a couple of numbers from the same source. How frequently will each digit 1 .. 9 appear? We humans usually assume the leading digits are equally likely. However that is often not the case at all. The digit 1 is much more likely than the digit 2, the digit 2 is more likely than 3, and so on down to 9. Why is that?! There are a lot of explanations for that, which go under Benford's Law.
Not all data sources follow Benford's law but often when the data is the outcome of an exponential growth process, like financial data, then the law applies. Imagine you pick a number 1 .. 9 equally likely, let's start with 1. Now doubling a number with a leading 1 will lead to a number with a leading 2 or 3 equally likely. However when the first digit is one of 5,6,7,8,9 then the next leading digit has to be 1. This should give you an intuition for why this phenomena occurs. A great explanation of the law can be found in this maths.org article.
Detecting fraud
As often with fraud detection, it boils down to humans being terrible at coming up with random numbers. Sometimes you can catch fraudulent activities by the opposite idea: people trying to be too random because they do not understand the underlying data generating process. This is exactly why Benford's Law can be effective: when data is expected to follow the law but it does not at all then something is fishy.
What do we expect to see if we apply this to Bitcoin exchange data?
I wrote a few of lines of Python (inspired by this article) which applies the law to a couple of days of BTC-E non-zero price returns. It's very nice to see how well Benford's expected distribution almost exactly matches the trade data.
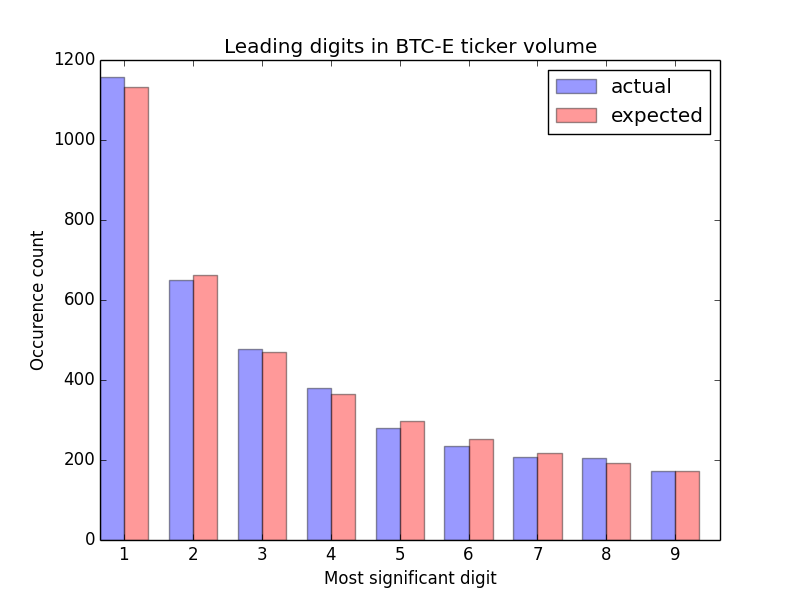
We can see how the leading digit 1 appears about 30% of the time and all other leading digits decay nicely, almost exactly matching as expected by Benford's Law. This result gives us some confidence that the reported volume has been generated by the natural trading process. If the actual numbers did not fit at all (and there's statistical tests to quantify this) then this would raise some concerns about the authenticity of the data.
Please feel free to run the same script against your favorite exchange data! Get the code here.
comments powered by Disqus